www.MegaLab.it

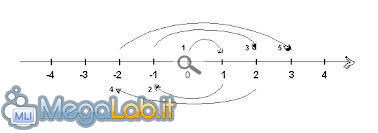
Un PRNG crittografico, come spiegato nei precedenti articoli, è in grado di generare sequenze di byte casuali, rispondendo in tal modo al compito per il quale viene utilizzato e soddisfando pertanto la richiesta di casualità inoltrata all'incombenza. Possono però determinarsi delle circostanze nelle quali è indispensabile selezionare un elemento casuale da un insieme e ciò comporta ulteriori ed elaborati approcci che debbono essere formalizzati con estrema attenzione.

La scelta di un elemento casuale impone che questa avvenga in modo altrettanto fortuito ed uniformemente da un insieme che sia assolutamente referenziato: ciò implica che ogni singolo elemento deve godere della medesima possibilità ad essere selezionato, con una deviazione dalla probabilità uniforme quantificabile in 2^-128 alfine di ottenere un livello di sicurezza che raggiunga i 128 bit. Tale operazione non è affatto semplice e non sempre si riesce ad eseguirla nella giusta maniera, come avremo modo di osservare nel prosieguo dell'articolo.

Proviamo a supporre l'esistenza di n come il numero degli elementi nel nostro insieme dal quale effettuare la selezione descritta. Come esempio tentiamo la scelta di un elemento da un insieme così definito: 0, 1... n -1, se tale operazione giunge a buon fine siamo in grado di selezionare gli elementi dall'interno di qualsivoglia insieme con dimensione di n.

Analizziamo adesso alcuni casi reali e didatticamente indispensabili per capire i concetti appena esposti:

• n = 0 non esistono chiaramente degli elementi, pertanto si otterrà un errore

• n = 1 un elemento singolo non consente alcuna selezione

• n = 2^k in questo caso si ottengono k bit di dati casuali dal nostro PRNG interpretabili come un numero che appartiene all'intervallo 0, ... n -1 e quindi uniformemente casuale. È anche possibile acquisire un numero intero di byte dal nostro PRNG, tralasciando alcuni bit appartenenti all'ultimo byte.

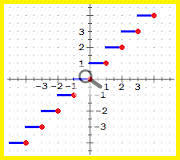
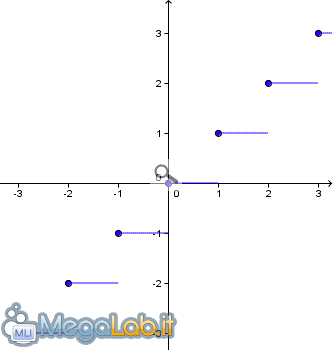
A questo punto è necessario discutere il caso in cui n non dovesse risultare potenza di 2: una soluzione potrebbe consistere nel selezionare un intero casuale di 32 bit interpretandolo come modulo n. Osserviamo, ad esempio n = 5 e procediamo con m: = |2^32/|, se acquisiamo un numero pari a 32 bit uniformemente casuale, riducendolo a modulo 5, il risultato inerente 1, 2, 3, 4 otterrà una probabilità m/2^32 mentre un risultato pari a 0 potrà verificarsi con una probabilità di (m + 1) /2^32 con una deviazione contenuta ma che potrebbe evolversi significativamente.

Il modo migliore per selezionare un numero casuale consiste nel basare il proprio operato su prove ed errori, ad esempio, per produrre un valore casuale nell'intervallo 0, ... 4 è necessario generare prima un valore casuale nell'intervallo 0, ... 7, fattibile chiaramente, ponderato che 8 è una potenza di 2. Se il prodotto è uguale o maggiore di 5 verrà ignorato e si procede alla selezione di un nuovo numero casuale sempre nell'intervallo 0, ... 7, proseguendo fintanto che non si trova il numero desiderato all'interno dell'intervallo prestabilito.

Per meglio capire l'operazione descritta ricorriamo ad uno schema che prevede la selezione di un numero casuale da un intervallo comprendente 0, ..., n -1 con n ≥ 2

• Supponiamo k come intero minore tale che 2^k ≥ n

• Il PNRG produce un numero casuale K avente k bit compreso nell'intervallo 0, ..., 2^k -1

• Se K = ≥ n il PRNG ripete l'operazione

• Il numero K è il risultato desiderato

In apparenza l'operazione parrebbe farraginosa, in effetti dovranno essere ignorati praticamente la metà dei numeri generati, ma è comunque suscettibile di adeguamento, ponderato che 2^32 -1 è un multiplo di 5, selezionare quindi un numero casuale nell'intervallo 0, ..., 2^32 -2 considerando come risposta il risultato modulo 5. Attenzione: per acquisire un valore appropriato nell'intervallo 0, ..., 2^32 -2 utilizziamo il medesimo sistema basato su prove ed errori, con la sostanziale differenza che, nel caso specifico, la possibilità di dover ignorare valori intermedi risulta molto più contenuta.

La formulazione generale indica di selezionare un k che conviene, tale che 2^k ≥ n, pertanto definiamo q: = |2^k/n| e così selezioniamo un valore casuale r nell'intervallo 0, ..., nq -1 con il medesimo approccio basato su prove ed errori fino ad ottenere un r desiderato che produrrà il risultato finale come (r mod n).

Mariano Ortu vi saluta dalla terra dei nuraghi!