Canali
Ultime news

Ultimi articoli
 Le ultime dal Forum |
Il pezzo che stai leggendo è stato pubblicato oltre un anno fa.
 La trattazione seguente è piuttosto datata. Sebbene questo non implichi automaticamente che quanto descritto abbia perso di validità, non è da escludere che la situazione si sia evoluta nel frattempo. Raccomandiamo quantomeno di proseguire la lettura contestualizzando il tutto nel periodo in cui è stato proposto. La trattazione seguente è piuttosto datata. Sebbene questo non implichi automaticamente che quanto descritto abbia perso di validità, non è da escludere che la situazione si sia evoluta nel frattempo. Raccomandiamo quantomeno di proseguire la lettura contestualizzando il tutto nel periodo in cui è stato proposto.
Esistono svariate soluzioni legate ai PRNG, alcune molto valide ed altre meno. In questo articolo osserviamo come dovrebbe essere la struttura funzionale di un generatore definito forte crittograficamente. Tendenzialmente le componenti che formano l'impalcatura di un buon PRNG crittografico dovrebbero essere tre:
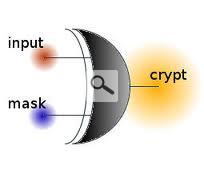
Analizziamo adesso in dettaglio il primo dei componenti descritti per comprendere, nella sua completezza, quanto sia importante ed il ruolo che svolge all'interno di un PRNG crittografico. Generatore: alchimia dei numeri casuali Come nei precedenti articoli accennato, il generatore è il commutatore di un dato stato avente lunghezza fissa con dati in uscita a lunghezza mutevole. La realizzazione di un generatore passa attraverso un codice a blocchi, all'occorrenza l'algoritmo Twofish assolve magnificamente il compito: lo stato interno sarà composto da una chiave a 256 bit ed un contatore a 128 bit. In virtù di quanto sopra esposto diciamo che il generatore deve referenziarsi come un codice a blocchi in modalità CTR, quest'ultima rappresenterà i dati casuali in uscita. Quando sussiste una richiesta di dati casuali, il generatore avrà il compito di soddisfarla producendo i dati pseudocasuali necessari: se un malintenzionato riuscisse nella compromissione dello stato interno successivamente alla richiesta in oggetto, è importante cautelarsi affinché non abbiano ad essere bruciati anche i precedenti output del generatore. Per far ciò si possono produrre, post singola richiesta, ulteriori 256 bit addizionali di dati pseudocasuali da utilizzare come chiave ex novo in relazione allo stato interno. La tecnica consente di accantonare la chiave reale ed evitare così che vengano acquisite informazioni inerenti le richieste precedenti. La garanzia che i dati generati siano esplicitamente casuali è data dalle modeste dosi per ogni ciclo, infatti quando si tratta di dati effettivamente casuali potrebbero verificarsi dei blocchi ripetuti, evento questo che viene scongiurato nella modalità CTR. Qualche soluzione al problema è attuabile, come il ricorso alla sola metà di un blocco cifrato oppure utilizzare una funzione pseudocasuale invece che il codice a blocchi. Una tra le soluzioni più semplici consiste nella limitazione del numero di byte di dati casuali prodotti ad ogni richiesta: ciò dovrebbe complicare l'analisi della deviazione statistica che viene a prodursi utilizzando solamente metà di un blocco cifrato. Parrebbe una buona soluzione l'utilizzo di SHA - 256 anche se ciò andrebbe a scapito dell'efficienza: teoricamente è possibile affermare che l'utilizzo di un buon PRNG crittografico, dal punto di vista della velocità, potrebbe risultare addirittura svantaggioso, in virtù del fatto che, rallentare il PRNG medesimo alfine di guadagnare una manciata di bit di sicurezza addizionali produrrebbe un pessimo generatore ed in conseguenza un crollo verticale della sicurezza globale del sistema. Soffermiamoci adesso a capire il perché di quanto affermato. Supponiamo di generare 2 elevato 64 blocchi di uscita da una singola chiave: ci si deve in questo caso preparare ad una collisione nei valori dei blocchi, infatti il reiterare di alcune delle richieste aventi tali dimensioni, paleserebbe la non perfetta casualità dell'output dovuta all'assenza delle collisioni previste. Limitando le richieste ad una dimensione pari a 2 elevato 16 blocchi, quindi 2 elavato 20 byte, e disponendo di un generatore al top, la possibilità che avvenga una collisione di blocchi in 2 elevato 16 blocchi di uscita è quantificabile attorno a 2 elevato -97, ragion per cui la completa assenza di collisioni non sarebbe percepibile fino a 2 elevato 97 richieste. In virtù di ciò è possibile quantificare gli sforzi di un malintenzionato intorno a 2 elevato 113 operazioni, il che rappresenta indubbiamente una cifra ragionevole. Il problema non si porrebbe utilizzando un codice a blocchi pari a 256 bit poiché le collisioni non rappresenterebbero difficoltà alcuna: l'attaccante dovrà spendersi in 2 elevato 113 operazioni di approccio ed anche il sistema che subisce dovrà effettuare altrettante codifiche. Ciò significa che l'assalto descritto è praticamente a carico del computer sotto attacco in termini di velocità esecutiva. Nel caso citato, quando viene creata la chiave ex novo dopo ogni richiesta di output, è buona norma evitare di azzerare il contatore, serve ad evitare problemi in presenza di eventuali cicli brevi. Se venisse a ripetersi il valore della chiave ed ogni volta procediamo all'azzeramento, avendo le richieste dimensione fissa, la logica conseguenza sarebbe che anche la successiva chiave verrebbe reiterata, entrando in tal modo in un ciclo, seppur breve, di chiavi identiche. Per evitare questa improbabile ma possibile situazione, come in precedenza accennato, non si deve azzerare il contatore, approfittando del fatto che questi consta di 128 bit e quindi mai verrà a ripetersi un valore pari a 2 elevato 128 blocchi che va oltre la capacità di calcolo prevista. Future ipotesi verranno chiaramente vagliate e adeguate alla potenza di calcolo disponibile! Altro importante accorgimento è quello di indicare il valore 0 al contatore quando il generatore non dispone ancora di una chiave e pertanto non potrà produrre alcuna uscita. Si tenga presente che il limite di ogni singola richiesta ad un massimo di 1 MB di dati non è chiaramente rigorosa, qualora si ha bisogno di oltrepassare tale restrizione è possibile reiterare le richieste. Mariano Ortu vi saluta dalla terra dei nuraghi! Segnala ad un amico |
- Unisciti a noi
- | Condizioni d'uso
- | Informativa privacy
- | La Redazione
- | Info
- | Pressroom
- | Contattaci
© Copyright 2025 BlazeMedia srl - P. IVA 14742231005
- Gen. pagina: 0.44 sec.
- | Utenti conn.: 137
- | Revisione 2.0.1
- | Numero query: 44
- | Tempo totale query: 0.1